Խորեն Սարգսյանի բլոգ

Մխիթար Սպարապետ

Գ.Մխիթարյանի <<Գիտելիքների ստուգման առաջադրանքներ մաս II  >>-ից էջ3 -ից մինչև էջ8 -ի տարբերակները։

1․ Այն էներգիան, որով մարմինը օժտված է իր շարժման հետևանքով, անվանվում է կինետիկ էներգիա։

2․ Սեղմված զսպանակի էներգիան պոտենցիալ էներգիայի օրինակ է։

3․ Գիրքը դրված է սեղանին։ Հատակի նկատմամբ այն օժտված է պոտենցիալ էներգիայով

4․Բրատսկի ՀԷԿ-ում ամբարտակից առաջ և նրանցից հետո ջրի մակարդակների տարբերությունը 100մ է։ Ի՞նչ էներգիայով է օժտված ամբարտակում գտնվող ջուրը։

Պատ․՝ Պոտենցիալ

5․

6․

7․

Հարցեր և առաջադրանքներ։

1․ Ո՞ր  շրջանագիծն  է  կոչվում  բազմանկյանը  արտագծյալ:    

Եթե բազմանկյան բոլոր գագաթները գտնվում են շրջանագծի վրա, ապա շրջանագիծը կոչվում է այդ բազմանկյան արտագծյալ շրջանագիծ:

2․ Քանի՞  շրջանագիծ  կարելի  է  արտագծել  տրված  եռանկյանը:

2

3․ Հնարավո՞ր  է  արդյոք  ցանկացած  քառանկյան  արտագծել  շրջանագիծ: 

Ոչ

4․ Ի՞նչ  հատկություն  ունի  շրջանագծին  ներգծված  քառանկյունը:

Եթե քառանկյանը կարելի է շրջանագիծ արտագծել, ապա տեղի ունի հետևյալ հատկությունը՝ Ցանկացած ներգծյալ քառանկյան հանդիպակաց անկյունների գումարը 180⁰ է:

5․Սեղանին արտագծված է շրջանագիծ: Հաշվիր սեղանի մյուս անկյունները, եթե անկյուններից մեկը՝ F=10° է:

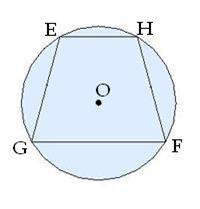
<G=<F=10^o
<E=<H=180^o-10^o=170^o

6․ Գտնել B և D անկյունները։

Ցանկացած ներգծյալ քառանկյան հանդիպակաց անկյունների գումարը 180⁰ է:
<D=180^o-117^o=63^o
<B=180^o-85^o=95^o

7․ O կենտրոնով շրջանագծին ներգծված է ZXY եռանկյունն այնպես, որ ZX-ը  տրամագիծ է։ ZY աղեղի աստիճանային չափը հավասար է 104⁰ -ի։ Գտնել ZXY եռանկյան անկյունները։

<Y=90^o, քանի որ՝ ZX շրջանագծի տրամագիծն է, U ZX=180^o
U XY=180^o-104^o=76^o
Ուղղանկյուն եռանկյան դեպքում, արտագծյալ շրջանագծի կենտրոնը գտնվում է եռանկյան ներքնաձիգի վրա:
<X=Y:2=45^o
<Z=180^o-(90^o+45^o)=45^o

8․ Օգտվելով գծագրից, գտնել ∠ B-ը։

AB տրամագիծ է և աղեղ AB=180^o=>
<C=90^o
<B=180^o-(90^o+46^o)=44^o

9․ Գտնել ∠ R-ը և ∠B-ն։

<R=180^o-74^o=106^o
<B=180^o-92^o=88^o

10․ ABC եռանկյանը արտագծված է շրջանագիծ։ Գտնել այդ շրջանագծի շառավիղը, եթե AC=24 սմ, ∠A=60⁰, ∠B=30⁰:

Եթե, ∠A=60⁰, ∠B=30⁰, ապա <C=90^o
Ուղղանկյուն եռանկյան դեպքում, արտագծյալ շրջանագծի կենտրոնը գտնվում է եռանկյան ներքնաձիգի վրա:
Ուղղ. եռ. էջ AC=24 սմ, գտնվում է 30^o-ի դիմաց հետևաբար ներքնաձիգ      

AB= 2AC=48սմ և տրամագիծ է:
R=48:2=24սմ

11. Արդյոք կարելի՞ է տրված ABCD քառանկյանը արտագծել շրջանագիծ, եթե ա)∠A=64⁰, ∠ B=95⁰, ∠C=106⁰բ) ∠A=72⁰, ∠B=69⁰, ∠D=111⁰ գ) ∠A=90⁰, ∠C=90⁰, ∠D=80⁰:

Եթե քառանկյան հանդիպակաց անկյունների գումարը 180° է, ապա նրան կարելի է արտագծել շրջանագիծ:

Այո, կարելի է:

Թեմա՝ Թվային անհավասարությունների հատկությունները:

Իրական թվերի կանոնները

Իրական թվերը ենթարկվում են հետևյալ կանոններին:

1 -ին կանոն: Ցանկացած երկու a և b իրարից տարբեր իրական թվերից մեկը մյուսից մեծ է: Այսինքն, ցանկացած a և b իրական թվերի համար տեղի ունի հետևյալ առնչություններից միայն մեկը՝ a=b, a>b, a<b

Օրինակ՝ 10 և 15 թվերի համար ճիշտ է 10<15 անհավասարությունը, և սխալ են մյուս երկու առնչությունները՝ 10=15 և 10>15 

2 -րդ կանոն: Ցանկացած երկու a և b իրարից տարբեր իրական թվերի միջև կա երրորդ թիվը: Այսինքն`  եթե a<b, ապա գոյություն ունի այնպիսի c թիվ, որ տեղի ունի հետևյալ երկկողմանի անհավասարությունը՝ a<c<b

Օրինակ՝ 1.4 և 1.5 թվերի համար գոյություն ունի, օրինակ, 1.44 թիվը, այնպես, որ տեղի ունի հետևյալ երկկողմանի անհավասարությունը՝ 1.4<1.44<1.5 

3 -րդ կանոն: Ցանկացած երեք a, b և c իրական թվերի համար, եթե a<b և b<c, ապա a<c

Օրինակ՝ 10/11<1 և 1<6/5 անհավասարություններից բխում է 10/11<6/5 անհավասարությունը:

Թվի գումարումը և թվով բազմապատկումը 

1 -ին հատկություն: Եթե a>b, ապա a+c>b+c

Եթե անհավասարության երկու մասերին գումարել կամ հանել միևնույն թիվը, ապա անհավասարության նշանը չի փոխվի:

Օրինակ՝ 3<12 ճիշտ անհավասարության երկու մասերին գումարելով −2 թիվը, կստանանք ճիշտ անհավասարություն՝  1<10

2 -րդ հատկություն: Եթե a>b և k>0, ապա ak>bk

Եթե անհավասարության երկու մասերը բազմապատկել միևնույն դրական թվով, ապա անհավասարության նշանը չի փոխվի:

Օրինակ Գիտենք, որ 17,2<x<17,3: Դրտարկենք 2x -ը:

Կրկնակի անհավասարությունը դրական 2 թվով բազմապատկելիս ստացվում է միանուն անհավասարություն (նշանները չեն փոխվում):

17,2⋅2<x⋅2<17,3⋅2,     34,4<2x<34,6

3 -րդ հատկություն: Եթե a>b և k<0, ապա ak<bk

Եթե անհավասարության երկու մասերը բազմապատկել միևնույն բացասական թվով, ապա անհավասարության նշանը կփոխվի:

Օրինակ՝ Հայտնի է, որ 17,2<x<17,3: Դիտարկենք −2x-ը:

Կրկնակի անհավասարությունը բացասական −2 թվով բազմապատկելիս ստացվում է հականուն անհավասարություն (նշանները փոխվում են):

17,2⋅(−2)<x⋅(−2)<17,3⋅(−2),   −34,4>−2x>−34,6,   −34,6<−2x<−34,4

Առաջադրանքներ

1.Համեմատել

1. <

2. >

3. =

4.<

5.<

6.<

2. Երկու ճշմարիտ անհավասարությունների հիման վրա կատարել եզրակացություն.

-5 < 2

-2 < 2

2 > 0

2,(1) > 1,(6)

-3,7 > -7

0,(5) < 0,(67)

5/6 < 9/8

7/16 < 8/16

3.Նշել տրված թվերից մեկից մեծ և մյուսից փոքր թիվ: Պատասխանը գրել կրկնակի անհավասարության տեսքով:

3 < 4․5 < 5

-25 < -28․5 < -29

4.Գրել անհավասարություն, որը ստացվում է տված անհավասարության ձախ և աջ մասերի թվերը փոխարինելով նրանց հակադարձներով:

5. Տրված ճշմարիտ անհավասարությունից ստանալ ճշմարիտ անհավասարություն,որում յուրաքանչյուր թիվը փոխարինված է իր հակադիրով:

6. Տրված ճշմարիտ անհավասարությունից ստանալ նոր ճշմարիտ անհավասարություն` գումարելով նրա երկու մասերին միևնույն թիվը.

 ա)14<21  բ) 32> 27  գ) 45<78  դ) -55<88   ե) -5 > -15  զ) 64> -99

7. Տրված ճշմարիտ անհավասարությունից ստանալ նոր ճշմարիտ անհավասարություն` նրա երկու մասը բազմապատկելով միևնույն դրական թվով.

8. Բազմապատկել ճշմարիտ անհավասարության երկու մասը միևնույն բացասական թվով:

9. Համեմատել

1. Ի՞նչ է օքսիդացման աստիճանը և ինչպե՞ս է այն որոշվում:

Օքսիդացման աստիճանը մոլեկուլում կամ իոնում գտնվող ատոմի էլեկտրոնային վիճակի ցուցանիշն է։ Այն ցույց է տալիս, թե որքան էլեկտրոն է կորցնում կամ ստանում ատոմը իր կապի մեջ ներգրավված այլ ատոմներից։ Օքսիդացման աստիճանը որոշվում է օրենքների համաձայն՝ հաշվի առնելով մոլեկուլի կամ իոնի ընդհանուր խթանիչ տեմպերը։

2.Ինչպե՞ս է փոխվում մետաղների օքսիդացման աստիճանը օքսիդացման և վերականգնման ժամանակ:

Մետաղների օքսիդացման աստիճանը բարձրանում է օքսիդացման ժամանակ (երբ մետաղը կորցնում է էլեկտրոններ), իսկ վերականգնման ժամանակ՝ նվազում է (երբ մետաղը ստանում է էլեկտրոններ)։

3.Ինչո՞ւ է թթվածինը պերօքսիդներում (-1) օքսիդացման աստիճան ունենում, բայց սովորաբար (-2):

Թթվածինը պերօքսիդներում (-1) օքսիդացման աստիճան ունի, քանի որ դրանք ունեն երկու թթվածնային ատոմներ, որոնք կիսվում են էլեկտրոններով, և յուրաքանչյուրը ստանում է մեկ էլեկտրոն։ Այդ պատճառով այն ունի այսպես ասած «բարձրացնելված» օքսիդացման աստիճան՝ -1, չնայած սովորաբար սովորական օքսիդացման աստիճանը -2 է։

4.Գտե՛ք օքսիդացման աստիճանները հետևյալ միացություններում.

• H₂SO₄

• KMnO₄

• Fe₂O₃

• NH₄Cl

H₂SO₄. Օքսիդացման աստիճանները՝ H = +1, S = +6, O = -2KMnO₄.

Օքսիդացման աստիճանները՝ K = +1, Mn = +7, O = -2Fe₂O₃.

Օքսիդացման աստիճանները՝ Fe = +3, O = -2NH₄Cl.

Օքսիդացման աստիճանները՝ N = -3, H = +1, Cl = -1

5.Ընտրիր այն քիմիական տարրերի նշանները, որոնց նվազագույն օքսիդացման աստիճանը 0 է.
K, CI, N, H, Ca, Zn, O,C, S, Al, F:

Հարցեր և առաջադրանքներ։

1․ Գրել անկյան կիսորդի հատկությունը։

Անկյան կիսորդի ցանկացած կետ հավասարահեռ է անկյան կողմերից:

2․ Թվարկել եռանկյան նշանավոր կետերը։

Կիսորդների հատման կետը

Միջնագծերի հատման կետ(ծանրության կենտրոն)

Բարձրությունների հատման կետը (օրթոկենտրոն)

Միջնուղղահայացների հատման կետը

3․ Եռանկյան մեջ տարված են միջնագծեր և բարձրություններ: Դրանց վերաբերյալ թվարկված պնդումներից որ՞ն է ճիշտ:

ա Եռանկյան բարձրությունները հատվելիս բաժանվում են 4:1 հարաբերությամբ հատվածների:

բ Եռանկյան միջնագծերը հատվելիս բաժանվում են 2:1 հարաբերությամբ հատվածների:

գ Եռանկյան միջնագծերը հատման կետով բաժանվում են 3:2 հարաբերությամբ հատվածների:

դ Բոլոր պնդումներն էլ սխալ են:

4․ Ո՞ր  շրջանագիծն  է  կոչվում  բազմանկյանը  ներգծյալ։

Այն շրջանագիծը որը շոշափում է բազմանկյան բոլոր կողմերը։

5․ Նշել եռանկյունները, որոնց արտագծված է շրջանագիծ:

ա) PRT

բ) EFG

գ) KLM

դ) MNL

ե) ABC

զ) DEF

6․ ABC հավասարասրուն եռանկյան AB և BC կողմերին տարված բարձրությունները հատվում են M կետում: BM ուղիղը AC հիմքը հատում է N կետում: Որոշիր NC, եթե AC=36սմ

Քանի որ BN-ը անցնում է մյուս երկու բարձրությունների հատման կետով => ինքն էլ է բարձրություն։ Քանի որ հավասարասրուն եռանկյուն է => BN բարձրությունը նաև միջնագիծ է => NC=36:2=18

7․ Հաշվել քառանկյան անհայտ կողմը, եթե նրան ներգծված է շրջանագիծ: FG=10սմ, EH=15սմ, HG=12սմ

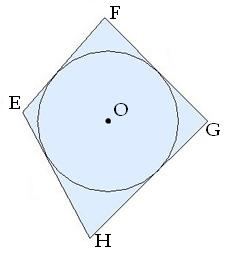
Ըստ քառանկյանը ներգծած շրջանագծի հատկության EF=10+15-12=13սմ

Թեմա՝ Թվաբանական գործողություններ իրական թվերի հետ։

a,b,c իրական թվերի համար տեղի ունեն գումարման և բազմապատկման ընդունված կանոնները՝

a+b=b+a    ab=ba     a+(b+c)=(a+b)+c   a(bc)=(ab)c    (a+b)c=ac+bc:

Տեղի ունեն նաև թվերի նշանների վերաբերյալ հետևյալ կանոնները՝ 

— երկու դրական թվերի արտադրյալը (քանորդը) դրական թիվ է,
— երկու բացասական թվերի արտադրյալը (քանորդը) դրական թիվ է,
— դրական և բացասական թվերի արտադրյալը (քանորդը) բացասական թիվ է: 

Թվաբանական գործողությունները իրական թվերի հետ ունեն հետևյալ հատկությունները:

1. Ռացիոնալ թվերի հետ ցանկացած թվաբանական գործողության (բացի 0-ի վրա բաժանելուց) արդյունքում ստացվում է ռացիոնալ թիվ:

2. Իռացիոնալ թվերի հետ թվաբանական գործողության արդյունքում կարող է ստացվել ինչպես ռացիոնալ, այնպես էլ իռացիոնալ թիվ:

3. Ռացիոնալ և իռացիոնալ թվերի հետ թվաբանական գործողության (բացի 0-ի վրա բաժանելուց և բազմապատկելուց) արդյունքում ստացվում է իռացիոնալ թիվ:

Բերված կանոններն ու հատկությունները տեսական բնույթ ունեն: Հիշում ենք, որ իրական թվերը անվերջ տասնորդական կոտորակներ են: Այդ պատճառով, գործնականում, հարմար է թվաբանական գործողությունները կատարել մոտավոր հաշված (կլորացրած) կոտորակների հետ:

Երկու իրական թվերի գումարը (տարբերությունը) մոտավոր հաշվելու համար նախ այդ թվերը կլորացնում են նույն ճշտությամբ, ապա գումարում են (հանում են) ստացված մոտավորությունները: 

Օրինակ

Մոտավոր հաշվենք a=3.889217010203… և b=−1.260076(27)… թվերի գումարը մեկ հարյուրերորդականի ճշտությամբ: 

1) Կլորացնենք այս թվերը մեկ հարյուրերորդականի ճշտությամբ՝

a≈3.89,b≈−1.26:

2) Կատարենք գումարումը՝

a+b≈3.89+(−1.26)==3.89−1.26=2.63:

Երկու իրական թվերի արտադրյալը (քանորդը) մոտավոր հաշվելու համար նախ այդ թվերը կլորացնում են նույն ճշտությամբ, բազմապատկում են (բաժանում են) ստացված մոտավորությունները, ապա արդյունքը կլորացնում են նույն ճշտությամբ:

Օրինակ

Մոտավոր հաշվենք վերևի c=4.579(128) և 2.1122334455… թվերի  արտադրյալը մեկ հարյուրերորդականի ճշտությամբ:

1) Կլորացնենք այս թվերը մեկ հարյուրերորդականի ճշտությամբ՝

c≈4.58,d≈2.11:

2) Կատարենք բազմապատկումը՝

c⋅d≈4.58⋅2.11=9.6638:

3) Կլորացնենք բազմապատկման արդյունքը նույն ճշտությամբ՝

c⋅d≈9.66:

Այսպիսով, առավել անկանխատեսելի է այն դեպքը, երբ գործողությունները կատարվում են երկու իռացիոնալ թվերի հետ: Այս դեպքում արդյունքը կարող է լինել ինչպես ռացիոնալ, այնպես էլ իռացիոնալ թիվ:

Օրինակ

ա) √3⋅√3=3  իռացիոնալ թվերի արտադրյալը տալիս է ռացիոնալ թիվ:

բ) √3⋅√5=√15  իռացիոնալ թվերի արտադրյալը տալիս է իռացիոնալ թիվ:

Հիշենք, որ ցանկացած իրական թիվ անվերջ տասնորդական կոտորակ է՝

— ռացիոնալ թվերն անվերջ պարբերական կոտորակներ են, իսկ

— իռացիոնալ թվերը՝ անվերջ ոչ պարբերական կոտորակներ:

Ուստի, գործնականում, հարմար է թվաբանական գործողությունները կատարել մոտավոր հաշված (կլորացրած) կոտորակների հետ:

1) Երկու իրական թվերի գումարը (տարբերությունը) մոտավոր հաշվելու համար նախ այդ թվերը պետք է կլորացնել նույն ճշտությամբ, ապա գումարել (հանել) ստացված արդյունքները:  

2) Երկու իրական թվերի արտադրյալը (քանորդը) մոտավոր հաշվելու համար նախ այդ թվերը պետք է կլորացնել նույն ճշտությամբ, բազմապատկել (բաժանել) ստացված մոտավորությունները, ապա արդյունքը կլորացնել նույն ճշտությամբ:

Առաջադրանքներ

1․Մինչև 0,1 ճշտությամբ կլորացնել թվերը և հաշվել նրանց մոտավոր գումարն ու տարբերությունը, եթե

ա) a= 3,28 b= 0,11  բ) a=-7,17 b= -0,33 գ) a=2,7235 b=-3,42426  դ) a=2,7(3) b=3,4(2)

2․Մինչև 0,01 ճշտությամբ կլորացնել թվերը և հաշվել նրանց մոտավոր գումարն ու տարբերությունը, եթե

ա) a=1,4545 b=-1,203      բ) a=2,1264  b=-3,1145 

գ) a=-5,777 b= 2,536      դ) a=0,5642  b=-3,573                 

3․Մինչև 0,1 ճշտությամբ կլորացնել թվերը և հաշվել նրանց մոտավոր արտադրյալն ու քանորդը, եթե

ա) a=-2,435 b=1,923       բ) a=2,14564  b=0,78788 

գ) a=-5,768 b= 2,534      դ) a=0,56  b=0,(3)

4․Մինչև 0,01 ճշտությամբ կլորացնել թվերը և հաշվել նրանց մոտավոր գումարն ու տարբերությունը, եթե

ա) a=0,253 b=0,75        բ) a=3,5781  b=-0,08788 

գ) a=-0,045 b= -0,593      դ) a=4,(2)  b=1,(3)   ե ) a=0,(2) b=2

5.Նշել մի որևէ թիվ, որը գտնվում է տված թվերի միջև

ա) a=2,3 b=2,4     բ) a=3,2 b=3,(2)    գ) a=-3,15 b=-3,14

6․ Ճի՞շտ է արդյոք անհավասարությունը․

ա)  3,5+2,729<3,6+2,729    բ)  -3,21+0,(4)<-3+0,(4)    գ) -5,6+3,2>-5,1+3,(2)

դ) 3,7⋅0,8< 3,8⋅0,8       ե) -5,1⋅0,(3)< -5⋅0,(3)       զ) -3,(8)⋅0,5>-3,8⋅0,(5)