














Թեմա՝ Պատկերացում գլանի մասին։
Ծանոթանանք տարածական այնպիսի մարմինների, որոնց մեջ շրջանագիծը նրա մասն է և ունի կարևոր դեր։ Սահմանում ` Ուղղանկյունը նրա որևէ կողմի շուրջը պտտումից առաջացած տարածական մարմինը կոչվում է գլան։ Գլանը ստանալու համար ուղղանկյունը պտտում ենք մի կողմի շուրջ։



Շրջանների կենտրոններով անցնող ուղիղը կոչվում է գլանի առանցք, շրջանները՝ գլանի հիմքեր, իսկ դրանց շառավիղները՝ գլանի շառավիղներ:Գլանի առանցքն ընդգրկող հարթությունը գլանի հետ ունի ընդհանուր մաս, որը կոչվում է գլանի առանցքային հատույթ:Գլանի առանցքային հատույթը ուղղանկյուն է, որի երկու հանդիպակաց կողմերը հիմքի տրամագծեր են: Իսկ մյուս երկու տրամագծեր չհանդիսացող կողմերը կոչվում են ծնորդներ:Գլանի ծնորդները հավասար են:

Գլանի կողմնային մակերևույթի բացվածքը ևս ուղղանկյուն է:

Հարցեր և առաջադրանքներ։
1․ Ո՞ր պատկերն է կոչվում գլան։ GEOGEBRA ծրագրով գծել գլան:

2․ Ինչպե՞ս կարելի է ստանալ գլան։
Գլանը ստանալու համար ուղղանկյունը պտտում ենք մի կողմի շուրջ։
3․ Ո՞րն է գլանի առանցքը, հիմքերը, շառավիղը, առանցքային հատույթը և ծնորդը։
Շրջանների կենտրոններով անցնող ուղիղը կոչվում է գլանի առանցք, շրջանները՝ գլանի հիմքեր, իսկ դրանց շառավիղները՝ գլանի շառավիղներ: Գլանի առանցքն ընդգրկող հարթությունը գլանի հետ ունի ընդհանուր մաս, որը կոչվում է գլանի առանցքային հատույթ: Գլանի առանցքային հատույթը ուղղանկյուն է, որի երկու հանդիպակաց կողմերը հիմքի տրամագծեր են: Իսկ մյուս երկու տրամագծեր չհանդիսացող կողմերը կոչվում են ծնորդներ:Գլանի ծնորդները հավասար են:
4․ Ի՞նչ պատկեր է գլանի առանցքային հատույթը։
Գլանի առանցքային հատույթը ուղղանկյուն է։
5․Գլանի առանցքային հատույթը քառակուսի է: Գտեք գլանի ծնորդի և շառավիղի հարաբերությունը:
Եթե գլանի առանցքային հատույթը քառակուսի է, ապա գնալի ծնորդի և շառավիղի հարաբերությունը հավասար է 2:1:
6․ Գլանի առանցքային հատույթը 40սմ պարագծով մի ուղղանկյուն է, որի անկյունագծերը փոխուղղահայաց են: Գտեք գլանի շառավիղը:
r=15սմ
7․Գլանի առանցքային հատույթը մի ուղղանկյուն է, որի անկյունագիծը ծնորդ հանդիսացող կողմի հետ կազմում է 600-ի անկյուն: Գտեք այդ անկյունագիծը, եթե գլանի ծնորդի երկարությունը 6սմ է:
12սմ
8․ Գլանաձև բաժակը կիսով չափ լցված է թեյով: Գոլորիշիանալուց հետո թեյի հետքը մնացել էր բաժակի պատերին: Երկրաչափական ի՞նչ պատկեր է այդ հետքը:
Շրջանագիծ
9․ Գլանաձև ցիստեռնի մի մասը լցված է հեղուկով: Ի՞նչ պատկեր է հեղուկի մակերևույթը: Դիտարկեք ցիստեռնի տեղադրման երկու դեպք՝ ուղղաձիգ և հորիզոնական:
Առաջին դեպքում շրջանագիծ, երկրորդ դեպքում էլ ուղղանկյուն։
Թեմա՝ Առաջին աստիճանի մեկ անհայտով անհավասարումներ։
kx−b>0 կամ kx−b<0 տեսքի անհավասարումները, որտեղ k -ն և b -ն տրված թվեր են, ընդ որում k≠0, անվանում են առաջին աստիճանի մեկ x անհայտով անհավասարումներ:Օրինակ՝ 2 +>0,3-<0
k-ն անհավասարման անհայտի գործակից, իսկ b-ն ազատ անդամ։
Անհավասարման լուծումը այն թիվն է, որը x-ի փոխարեն տեղադրելով ստացվում է ճիշտ թվային անհավասարություն։
Լուծել անհավասարումը նշանակում է, գտնել նրա բոլոր լուծումները, կամ ապացուցել, որ դրանք չկան։
Օրինակ 1․ a−5<0, a<5 Պատասխան՝a∈(-∞;5)
Օրինակ 2․ −2y−100<0 Երկու մասը բաժանելով -2-ի, կստանանք՝
y>−50 (անհավասարության նշանը փոխվում է)
Պատասխան՝y∈(−50;+∞)
Հուշում՝ երբ թիվը կամ փոփոխականը անհավասարման մի մասից տեղափոխվում է մյուս մասը, ապա նրա նշանը փոխվում է:
Մեկ անհայտով առաջին աստիճանի անհավասարումների լուծման ալգորիթմը հետևյալն է՝ ա այդ անհավասարման ազատ անդամը տեղափոխում ենք անհավասարման աջ մասը, փոխելով նշանը հակադիրով, բ ստացված անհավասարման երկու մասը բաժանել անհայտի գործակցի վրա, ընդ որում, եթե >0, ապա անհավասարման նշանը չի փոխվում, իսկ եթե<0, ապա անհավասարման նշանը փոխվում է հակադիրով։ Ստացված անհավասարումը հենց պատասխանն է։
Հարցեր և առաջադրանքներ։
1․ Ի՞նչն են անվանում առաջին աստիճանի մեկ անհայտով անհավասարում։ Գրել մի քանի օրինակ։
2․ Ի՞նչն են անվանում առաջին աստիճանի մեկ անհայտով անհավասարման լուծում։
3․ Ի՞նչ է նշանակում լուծել առաջին աստիճանի մեկ անհայտով անհավասարումը։
4․ Արդյո՞ք 4 թիվը հանդիսանում է նշված անհավասարման լուծում՝
ա) x>0-Այո
բ) x<-2-Ոչ
գ) -4<x<4-Ոչ
դ) x<4,2-Այո
ե) 3,8 <x<4,1-Այո
5․ Լուծել անհավասարումները․

1.
ա) x ∈ ( 1 ; +∞ )
բ) x ∈ (-∞ ; -5 )
գ) x ∈ [0 ; 0,5)
դ) x ∈ [0 ; +∞)
ե) x ∈ [0 ; +∞)
զ) x ∈ [0 ; 1. 1/3)
2.
ա) x ∈ ( 3 ; +∞)
բ) x ∈ (-∞ ; 4 )
գ) x ∈ (0 ; +∞ )
դ) x ∈ ( -∞ ; 12 )
ե) x ∈ ( -2 ; +∞ )
զ) x ∈ (- ∞ ; -9 )
3.
ա) x ∈ ( 2,2 ; +∞ )
բ) x ∈ ( -∞ ; 7,5 )
գ) x ∈ ( -∞ ; 4,9 )
դ) x ∈ ( 1,4 ; +∞ )
ե) x ∈ ( 2,8 ; +∞ )
զ)???
6․ Լուծել անհավասարումները և լուծումը պատկերել թվային ուղղի վրա․

ա)

բ)

գ)

դ)

ե)
զ)
7․ Լուծել անհավասարումները և լուծումը պատկերել թվային ուղղի վրա․

ա)

բ)

գ)

դ)

ե)

զ)

8․ Լուծել անհավասարումները․

ա) x ∈ ( -∞; 6 )
բ) x ∈ (-∞ ; 1,(3) )
գ) …
դ) x ∈ ( -∞ ; 0 )
ե) x ∈ (-∞ ; 0,(3) )
զ) x ∈ (0,(36) ; +∞ )
9․ Լուծել անհավասարումները․

Թեմա՝ Կանոնավոր բազմանկյան ներգծյալ և արտագծյալ շրջանագծերը։
Ցանկացած կանոնավոր բազմանկյանը կարելի է ներգծել և արտագծել շրջանագծեր: Երկու շրջանագծերի կենտրոնները համընկնում են և կոչվում են կանոնավոր բազմանկյան կենտրոն:

Ներգծյալ շրջանագիծը շոշափում է բազմանկյան բոլոր կողմերը նրանց միջնակետերում։

Արտագծյալ շրջանագիծը անցնում է բազմանկյան բոլոր գագաթներով:
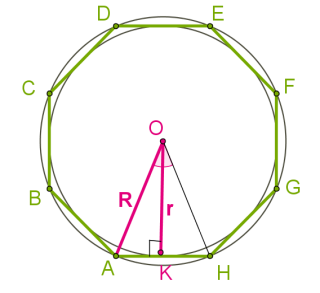
∡AOH=360°/n;∡AOK=360°/2n=180°/n


Հարցեր և առաջադրանքներ։
1․ Ո՞ր բազմանկյունն է կոչվում կանոնավոր։ Բերել օրինակներ
Ցանկացած կանոնավոր բազմանկյանը կարելի է ներգծել և արտագծել շրջանագծեր: Երկու շրջանագծերի կենտրոնները համընկնում են և կոչվում են կանոնավոր բազմանկյան կենտրոն:
2. GEOGEBRA ծրագրով գծել կանոնավոր եռանկյանը ներգծյալ և արտագծյալ շրջանագծեր։

3․GEOGEBRA ծրագրով գծել կանոնավոր քառանկյանը ներգծյալ և արտագծյալ շրջանագծեր։

4․Ճշմարի՞տ է արդյոք հետևյալ պնդումը․
ա) յուրաքանչյուր կանոնավոր բազմանկյուն ուռուցիկ բազմանկյուն է,
Այո
բ) ցանկացած ուռուցիկ բազմանկյուն կանոնավոր բազմանկյուն է։
Ոչ
5․Հետևյալ պնդումներից որո՞նք են ճշմարիտ․
ա) բազմանկյունը կանոնավոր է, եթե այն ուռուցիկ է, և նրա բոլոր կողմերը հավասար են,
Այո
բ) եռանկյունը կանոնավոր է, եթե նրա բոլոր անկյունները հավասար են,
Այո
գ) հավասար կողմերով յուրաքանչյուր քառանկյուն կանոնավոր քառանկլյուն է։ Պատասխանները հինմավորել։
Այո
6․ Տրված է 13,4 դմ կողմով EFGH քառակուսին:
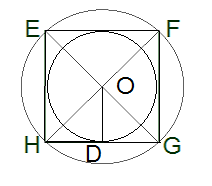
ա) Հաշվիր քառակուսուն ներգծված շրջանագծի շառավիղը:
13.4մ / 2 = 6.7դմ
բ) Հաշվիր քառակուսու մակերեսը:
13.4դմ * 13.4դմ = 179.56դմ^2
7․Տրված է հավասարակողմ եռանկյուն, BO=16սմ:
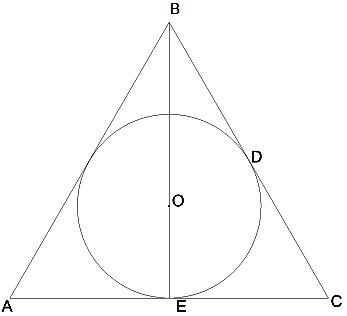
ա) Գտնել ներգծյալ շրջանագծի շառավիղը:
8սմ
բ)Գտնել հետևյալ հատվածների երկարությունները:
OE, BE, AD։
OE = 8սմ
BE = 8սմ
AD = 8սմ
1 урок




2 урок. Проверочная работа за февраль (выполнять на уроке)
Исследуй сначала слово с научной точки зрения , а потом посмотри, почувствуй, как живёт слово в сказке, маленьком рассказе, большой повести, в стихах и песнях, в нашей повседневной речи, как может ранить, обидеть человека или, наоборот, сделать его счастливым, подарить надежду, вселить веру в свои силы. Используй все типы словарей, энциклопедий, справочную литературу, помощь и советы учителя, родителей, друзей.
Копилка слов для работы в проекте: родина, жизнь, человек, детство, совесть, глаза, слёзы, руки, сердце, след, дорога, солнце, любовь, сказка, дом, мама,тайна, начало, портрет, дело, душа, зеркало, семья, характер, встреча, радость, чувство, мир, память.
Ход работы:
Создайте презентацию, отразите в ней свою работу.
1․ Նկարագրել սրտի կառուցվածքը,նշել նախասրտերը և փորոքները, սրտում գտնվող փականների տեսակները, դրանց ֆունկցիաները։

Սրտի աջ նախասրտի և աջ փորոքի բացվածքի սահմանում գտնվում են եռափեղկ փականներ (կազմված երեք փեղկից), իսկ ձախ նախասրտի ու ձախ փորոքի բացվածքի սահմանում` երկփեղկ փականները:
Սրտից դուրս եկող թոքային զարկերակի և աորտայի ներսում կան կիսալուսնաձև փականներ: Եռափեղկ և երկփեղկ փականները խոչընդոտում են արյան հետադարձ շարժումը փորոքներից նախասրտեր: Կիսալուսնաձև փականներն արգելակում են արյան հետադարձ շարժումը թոքային զարկերակից և աորտայից դեպի սիրտ:
2․Նկարագրել զարկերակների, երակների , մազանոթների կառուցվածքը, ֆունկցիաները, նշել հանդիպող բացառությունները։



Նպատակը․ ճոճանակի թելի երկարությունից տատանումների պարբերության և հաճախության կախվածության պարզաբանումը:
Անհրաժեշտ սարքեր և նյութեր․անցքով կամ կեռիկով գնդիկ,թել,ամրակալան՝կցորդիչով և թաթով,վայրկենաչափ կամ վայկենացույց,չափերիզ։
Աշխատանքի ընթացքը․Չափաժապավենով չափեցի 1.100սմ երկարությամբ թելը կախեցի նրանից կապեցի կեռիկով մետաղյա այն կախեցի արմակալանի կցոռթիչից այնպես որ (կստացվի թելավոր ճոճանակ),այն կախել այնպես,որ փոքր-ինչ սեղանից կամ գետնից բարձր լինի:Չափաժապավենով դրեցի գնդիկի տակ և շեղեցի հավասարակշռության դիրքից 8-ից 10սմ, և բաց թողեցի:Չափեցի 40 լրիվ տատանումների ժամանակը,բանաձևերով հաշվեցի տատանումների պարբերությունը և հաճախությունը:
Փորձի արդյունաբերություն՝
I=100մ
N=40
t=
v=N/T=
T=t/N=
Փորձը կրկնել՝ կարճացնելով թելը չորս անգամ,տատանումների լայնույթը դարձնելով 2սմ- ից 3սմ:
Անել եզրակացություններ՝ճոճանակի թելի երկարությունիցտատանումների պարբերության և հաճախության կախումների վերաբերյալ։
Փորձը տեսագրել ,պատրաստել տեսանյութ,տեղադրել բլոգներում
Չափաժապավենով
Առաջադրանքներ․
1)Անվանեք թվային բազմությանը պատկանող բոլոր ամբողջ թվերը՝
ա)[-3;1]
բ)(-3;1)
գ)[-3;1)
դ)(-3;1]
ե)[-2;3]
զ)(-2;3)
է)[-2;3)
ը)(-2;3]
2)Պատկերեք նշված բազմությունները թվային ուղղի վրա՝
ա)[3;5]
բ)(3;5)
գ)[3;5)
դ)(3;5]
ե)[-2;+∞)
զ)(-2;+∞)
է)(-∞;-2)
ը)(-∞;-2]
3)Պատկանու՞մ է արդյոք -2 թիվը թվային բազմությանը (գրառումը կատարեք ∈ և ∉ նշանների օգնությամբ):
ա)[-3;0]
բ)(-2;3)
գ)(-∞;-2]
դ)(-3;+∞)
ե)N
զ)Z
է)Q
ը)R
4)Անվանեք թվային բազմությանը պատկանող երեք ամբողջ թվեր՝
ա)[0;+∞)
բ)(0;+∞)
գ)(-∞;1)
դ)(-∞;1]
5)Գրառեք նշանակումը և պատկերեք նշված բազմությունները թվային ուղղի վրա՝
ա)2-ից 4 փակ միջակայքի (հատվածի)
բ)2-ից 4 բաց միջակայքի
գ)2-ից 4 կիսաբաց միջակայքի՝ 4-ը ներառած
դ)2-ից 4 կիսաբաց միջակայքի՝ 2-ը ներառած
ե)5-ից +∞ միջակայքի
զ)5-ից +∞ կիսաբաց միջակայքի
է) -∞-ից 0 միջակայքի
ը) -∞-ից 0 կիսաբաց միջակայքի
6)Պատկանու՞մ է արդյոք 2/3 թիվը թվային բազմությանը (գրառումը կատարեք ∈ և ∉ նշանների օգնությամբ):
ա)(0;1]
բ)[1;2]
գ)(-∞;2/3]
դ)(2/3;+∞)
ե)N
զ)Z
է)Q
ը)R
282.Ընդգծված երկրորդական նախադասություններն արտահայտի՛ր համապատասխան բառակապակցություններով (դերբայական դարձվածներով):
Պահպանված կենդանիների մեջ կան տեսակներ, որոնք աննշան թիվ են կազմում:
Կան տեսակներ, որոնք աննշան թիվ են կազմում պահպանված կենդանիների մեջ:
Նա վերջին տիրակալն էր, որ իր երկրի անտառներում խոշոր կենդանիներ տեսավ:
Իր երկրի անտառներում խոշոր կենդանիներ տեսավ, նա վերջին տիրակալն էր:
Որքա՜ն զարմացավ նա, երբ բոլոր կողմերից գյուղերով շրջապատված անտառում եղջերուներ տեսավ:
Երբ բոլոր կողմերից գյուղերով շրջապատված անտառում եղջերուներ տեսավ, որքա՜ն զարմացավ նա:
Նա հույս ուներ, որ թեկուզ հեռվից կտեսնի արջին:
Նա թեկուզ հույս ուներ, որ հեռվից կտեսնի արջին:
Եթե կրկին անդրադառնանք ոչնչացված կենդանիների ցուցակին, կնկատենք առանձնապես տագնապալի մի հանգամանք:
Եթե կրկին անդրադառնանք ոչնչացված կենդանիների ցուցակին, տագնապալի մի հանգամանք կնկատենք առանձնապես:
284.Ընդգծված երկրորդական նախադասությունները դարձրո՛ւ դերբայական դարձվածներ:
Այն մարդկանց անունները, որոնք հաղթանակներ են տարել, նվաճելով օտար հողեր ու երկրներ, որոնք հաջողությամբ ոչնչացրել են իրենց դասակարգային,կրոնական կամ գաղափարական հակառակորդներին, հավերժացվել են պատմության հուշամատյաններում:
Նվաճելով օտար հողեր ու երկրներ, որոնք հաջողությամբ ոչնչացրել են իրենց դասակարգային, կրոնական կամ գաղափարական հակառակորդներին, այն մարդկանց անունները, որոնք հաղթանակներ են տարել, հավերժացվել են պատմության հուշամատյաններում:
ժողովուրդները զորավարներին հուշարձաններ են կանգնեցնում, պսակներ դնում անհայտ զինվորների շիրիմներին:
Ժողովուրդները հուշարձաններ են կանգնեցնում զորավարներին, պսակներ դնում անհայտ զինվորների շիրիմներին:
Բայց նրանք, ովքեր հող են վարում սառը տունդրայում կամ արևադարձային ջունգլիներում, համարյա միշտ կյանքից գնում են առանց հետք թողնելու:
Բայց նրանք համարյա միշտ կյանքից գնում են առանց հետք թողնելու, ովքեր հող են վարում սառը տունդրայում կամ արևադարձային ջունգլիներում:
Այսօր ո՞վ է հիշում նրանց, որ ջրանցքների ու ճանապարհների կառուցման ժամանակ են զոհվել:
Ո՞վ է հիշում նրանց այսօր, որ ջրանցքների ու ճանապարհների կառուցման ժամանակ են զոհվել:
Եվ, այդուհանդերձ, երբ նայում ենք Երկրին, չենք կարող նրանով չհիանալ:
Եվ այդուհանդերձ, չենք կարող նրանով չհիանալ, երբ նայում ենք Երկրին:
Մեր սիրտը ջերմանում է, երբ մտածում ենք, որ մարդը` Երկրի համեմատությամբ այդ անսահման փոքր էակը, իր մահկանացու ձեռքով անդադրում աշխատում է, որ մեր մոլորակի կերպարանքը փոխի:
Երբ մտածում ենք, որ մարդը՝Երկրի համեմատությամբ այդ անսահման փոքր էակը, իր մահկանացու ձեռքով անդադրում աշխատում է, մեր սիրտը ջերմանում է, որ մեր մոլորակի կերպարանքը փոխի:
283.Ընդգծված երկրորդական նախադասություններն արտահայտի՛ր դերբայական դարձվածներով:
Մեր կենդանաբանական այգու գոյության հինգ տարիների ընթացքում համառորեն հավաքում էինք այն կենդանիներին, որոնք իրենց հայրենիքում բնաջնջվում էին:
Համառորեն հավաքում էինք այն կենդանիներին, որոնք իրենց հայրենիքում բնաջնջվում էին, մեր կենդանաբանական այգու գոյության հինգ տարիների ընթացքում:
Հատկապես գորիլաներով էինք հպարտանում, որովհետև նրանք մեր ամենահետաքրքիր նմուշներն էին:
Հատկապես հպարտանլւմ էինք գորիլաներով, որովհետև նրանք մեր ամենահետաքրքիր նմուշներն են:
Միշտ հնարավոր չէր լինում գտնել կամ որսալ այն կենդանուն, որը մեզ հարկավոր էր:
Միշտ հնարավոր չէր այն կենդանուն գտնել կամ որսալ, որը մեզ հարկավոր էր:
Բինտուրոնգը, որն արջի նման է ու կառչուն պոչ ունի, շատ յուրօրինակ կենդանի է ու ապրում է Արևելյան Ասիայում:
Բինտուրոնգը շատ յուրօրինակ կենդանի է, որն արջի նման է ու կառչուն պոչ ունի, ապրում է Արևելյան Ասիայում:
Ակնոցավոր արջը, որի անունը Պեդրո կնքեցինք, Հարավային Ամերիկայից էր:
Ակնոցավոր արջը Հարավային Ամերիկայից էր, որի անունը Պեդրո կնքեցինք:
Երբ եկավ մեզ մոտ, պստլիկ քոթոթ էր` որսկան շան չափ:
Երբ եկավ մեզ մոտ, որսկան շան չափ՝պստլիկ քոթոթ էր:
Աշխարհում ամենից շատ սիրում էր, որ կանգնում էր ետևի թաթերի վրա, առջևի թաթերը ճաղերից դուրս հանում ու շոկոլադ ստանում:
Որ կանգնում էր ետևի թաթերի վրա, աշխարհում ամենից շատ սիրում էր, առջևի թաթերը ճաղերից դուրս հանում ու շոկոլադ ստանում:
Որպեսզի Պեդրոն ինչ-որ բանով խաղա, վանդակի առաստաղից անտակ տակառ էինք կախել:
Վանդակի առաստաղից անտակ տակառ էինք կախել, որպեսզի Պեդրոն ինչ-որ բանով խաղա:
Երբ Պեդրոն տխրում էր, մտնում էր իր տակառը, պառկում այնտեղ ու թաթը ծծում:
Մտնում էր իր տակառը, պառկում այնտեղ ու թաթը ծծում, եերբ Պեդրոն տխրում էր:
285.Ընդգծված դերբայական դարձվածները դարձրո՛ւ երկրորդական նախադասություններ:
Այստեղ արդեն երևակայության սահմաններից դուրս տանող այդ ճանապարհը դառնում է ավելի ուղիղ ու լայն:
Երևակայության սահմաններից դուրս տանող այդ ճանապարհը դառնում է ավելի ուղիղ և լայն:
Հետաքրքիր հետազոտությունների ճանապարհները` այժմ մի փոքր տրորված,մեկ կորչելով, մեկ երևան գալով, նորից հեռուն են տանում:
Այժմ մի փոքր տրորված, հետազոտությունների հետաքրքիր ճանապարհը, մեկ երևան գալով, նորից հեռուն են տանում:
Այդ մարդը կենդանիներն ու բույսերը վերափոխելու նպատակ ունի:
Այդ շարդը նպատակ ունի կենդանիներն ու բույսերը վերափոխելու:
Այնտեղ արդեն լսել էին քիմիական եղանակով կենդանի էակներ ստանալումասին:
Քիմիական եղանակով այնտեղ արդեն լսել էին, կենդանի էակներ ստանալումասին:
Մի՞թե մտածող մարդն անտարբեր կմնա` հանդիպելով այդ ճանապարհներիցմեկին:
Մտածող մարդն մի՞թե անտարբեր կմնա՝հանդիպելով այդ ճանապարհներից մեկին:
Մարդիկ առաջ են շարժվում նրանցով` բացելու համար նոր հորիզոններ:
Բնության մեծ գաղտնիքը` կյանքի ծագումը, գուշակելու համար ինքն իրեն բանտարկել էր փորձասենյակում:
Բնության գաղտնիքը ինքն իրեն բանտարկել էր փորձասենյակում՝կյանքի ծագումը, գուշակելու համար:
286.Ընդգծված դերբայական դարձվածները դարձրո՛ւ երկրորդական նախադասություններ:
Օվկիանոսի գաղտնիքների մասին ոչ մի պատմություն լրիվ չի լինի առանց անձնակազմի կողմից լքված «Մերի Սելեսթ» նավի պատմության: Հակառակ Ազորյան կղզիների և Պորտուգալիայի միջև հայտնաբերվելուն նավն ավելի հաճախ Բերմուդյան եռանկյունու գաղտնիքի հետ է կապվում: 1872 թ.դեկտեմբերի 4-ին «Դեի Գրատիա» բեռնանավը հայտնաբերեց նոյեմբերի 7-ին Նյու Յորքից դուրս եկած և դեպի Ճենովա ուղղություն վերցրած «Մերի Սելեսթը»: Առագաստանավը տեսնելով` բեռնանավի կապիտանը վատ նախազգացում ունեցավ նրա զիգզագ ընթացքի պատճառով: Նա հրամայեց մի խումբ նավաստիների բարձրանալ «Մերի Սելեսթի» վրա: Նավաստիները պիտի իմանային պատահածի մասին և տեղեկացնեին: Նրանք պարզեցին նավի դատարկ լինելը: Չկային կապիտան Բրիգսը, նրա կինն ու աղջիկը, ութ մարդուց բաղկացած անձնակազմը:
Նավի վրա ամեն ինչի կարգին լինելը և նավի` եղանակից տուժած չլինելը «Մերի Սիլեսթի» մասին բոլոր պատմողներն էլ վկայում են: Անձնակազմի ճակատագրի մասին վարկածներից ոչ մեկը փաստերով չի հաստատվել: Եվ այսօր Էլ այդ առեղծվածի մասին գիտենք օվկիանոսում հայտնաբերվելու օրվա չափ:
Խնդիր 1

Ոչ զրոյական իրարից տարբեր 6 թվանշաններ գրված են վանդակներում այնպես, որ 4 վանդականոց շարքի թվերի գումարը հավասար է 12, իսկ 3 վանդականոց սյան թվերի գումարը՝ 23։ Գտե՛ք բոլոր վանդակների թվերի գումարը։

Խնդիր 2

Նկարում առաջին պատկերը կազմված է 1 վանդակից, երկրորդը՝ 5, երրորդը՝ 13, չորրոդը՝ 25 և այդպես շարունակ։ Գտե՛ք 101-րդ պատկերում վանդակների քանակը։
1012+1002 = 20201
Խնդիր 3
1, 2, 3, 4 թվերը տեղադրված են a, b, c, d թվերի փոխարեն այնպես, որ տեղի ունի 𝑎/𝑏 − 𝑐/𝑑 = 1
հավասարությունը։ Գտե՛ք 𝑎 + 𝑐-ի արժեքը։
3/1 — 4/2
a=3
c=4
a+c=7
Խնդիր 4
Հնարավո՞ր է արդյոք 9 × 9 տախտակի յուրաքանչյուր վանդակում գրել 1 կամ 2, այնպես որ ցանկցած սյունում գրված թվերի գումարը բաժանվի 5-ի, իսկ ցանկցած տողում գրված թվերի գումարը՝ 7-ի։
| 1 | 2 | 2 | 1 | 2 | 2 | 2 | 1 | 1 |
| 1 | ||||||||
| 1 | ||||||||
| 1 | ||||||||
| 1 | ||||||||
| 1 | ||||||||
| 1 | ||||||||
Անհնար է